Calculation of the average return
In calculating the average return on their investments, pension providers follow a uniform guideline approved by the industry's joint investment reporting group.
Content of this page
Calculating the average nominal rate of return
The regulations issued by the Financial Supervisory Authority for earnings-related pension insurers in the private sector include rules for calculating the nominal returns on investments for periods of at most one year. The period is a calendar year or the first 1–3 quarters of the same calendar year.
According to the regulations, the return is calculated using the modified Dietz method, i.e. the rate of return is time and money weighted (MWR).
The Financial Supervisory Authority requires that the return data be published for the first six months of each year and for the calendar year. In accordance with the recommendation issued by the Investment Reporting Group, the largest actors in the earnings-related pension sector publish their return figures more frequently, i.e. after each quarter calculated from the beginning of the calendar year.
The Financial Supervisory Authority’s regulations concerning the publication of return figures do not apply to pension providers in the public sector. For the sake of consistency, they have also published the return figures for calendar years and for the first 1–3 quarters of each calendar year, calculated using the MWR method.
There are numerous situations where the insurer-specific average return is wanted for a period longer than one year although the authorities have not (yet) issued any regulations concerning calculation methods. TELA’s Return Calculation Group has therefore given instructions that an individual insurer’s nominal rate of return for a period exceeding one year is calculated as a geometric average (TWR) on MWR returns for whole years or quarters.
To be precise, the current recommendation only applies to periods that begin at a point in time that is not the start of a calendar year or end at a point in time that is not the end of a calendar year. For the sake of consistency, the same calculation method should also be used when the calculation period consists only of whole calendar years.
In addition to the MWR return, insurers are likely to calculate the TWR return figures for calendar years and their parts. However, the figures used in this recommendation as return figures for calendar years and their parts have been produced using the MWR method because, for instance for the above reasons, they are available in published form. When average returns are calculated over calendar years and their parts, the MWR method is not applied because in general it is difficult to determine the amount of capital employed over calendar years and their parts.
The above can be expressed formally by using the following symbols:
F(i,c,k) = insurer i’s return in monetary terms (cash return and changes in value) in investment category c during period k;
S(i,c,k) = insurer i’s capital employed in investment category c during period k, obtained using the MWR calculation method.
The quantity c may also be given the value “all investments”. The periods k are calendar years or the first 1–3 quarters of calendar years.
Thus, the figures f (i,c,k) = 100 * F (i,c,k ) / S (i,c,k) are the return figures that insurer i has reported for a calendar year or for certain quarters.
Return coefficients for the calculation period (“compound interest”) are composed as follows:
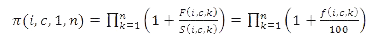
A “TWR-type” average return as per cent per year f(i,c,1,n) during n periods with a total duration of Y years is calculated as follows:
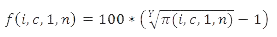
The result of formula (2) is rounded to the first decimal place.
The periods used are the longest times for which the capital employed is known in accordance with MWR calculation. In practice, this means whole calendar years or 1–3 quarters of the same calendar year. The periods are indexed backwards, starting from the last one. (Note: If the calculation period starts with a part of a calendar year, the first term of the product is obtained by dividing the return coefficient for the whole calendar year by the return coefficient of the quarters preceding the part included in the calculation.)
Example: To calculate the nominal rate of return for the period 30 September 2008–30 June 2011, the calculation period is the first and second quarter of 2011 + the year 2010 + the year 2009 + the fourth quarter of 2008, i.e. Y=0.5+1+1+0.25=2.75.
Group averages
Our website presents average nominal rates of return calculated for specific insurer groups or systems over calendar years.
The following symbols are used
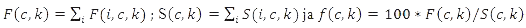
Modifying the MWR method, the annual average return for the calculation period is obtained as follows:
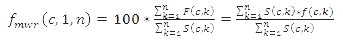
Thus, the annual average rate of return for the calculation period is the average of individual annual rates of return weighted with the capital employed.
The MWR method has only been used to calculate averages for periods consisting of whole calendar years.
Averages have also been calculated modifying the TWR method as follows:
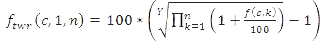
The TWR method can also be used for calculating real return averages for periods that have extra quarters at the beginning or end. If formula (4) has been applied, this is mentioned, for instance, in the footnote to the graph or table.
Calculating the average real rate of return
The authorities have not issued regulations about the calculation of real return, but there are various practices for this. In general, the prefix ‘real’ refers to how much the change in the original or nominal quantity and the change in prices differ from each other.
For example, the change in real wages means the difference between the change in nominal wages and the change in consumer prices. In connection with studies concerning, for instance, stock markets, the real return also refers to the difference between the return and the change in consumer prices. In the TyEL pension contribution level calculations conducted by the Finnish Centre for Pensions, the real return assumption refers to the difference between the returns and the change in consumer prices.
Statistics Finland publishes index figures describing the consumer price level every month. Thus, the price level prior to the return period is described by the price index value H(0) calculated for the immediately preceding month, while the price level at the end of the calculation period is described by index value H(m) calculated for the last month.
The real return is calculated from the total return, and there is no need to calculate it separately for each investment category. Let us examine a period of Y years consisting of periods 1,.,n. Insurer i’s nominal return coefficient for all investments is represented by (i,1,n). The nominal return coefficient is obtained by using formula (1). The coefficient “between” the coefficients for nominal return and the change in consumer prices is the real return coefficient. Thus
The real rate of return per year for the period 1–n (Y years) is
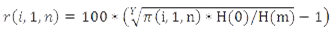
The result of formula (5) is rounded to the first decimal place.
From time to time, Statistics Finland changes the base year of the consumer price index. In consequence, the index values calculated from different base years must be linked in one way or another. However, each month Statistics Finland maintains and publishes a sufficiently long linked index series, the cost of living index (1951=100). The index values describing consumer prices are taken from this index series. The index values are available at the Statistics Finland website: Consumer price index.
Group averages
Our website presents average real returns calculated for specific insurer groups or systems over calendar years.
Adapting the MWR method over years, the nominal total returns in euros F(k) must be converted into real returns in euros for each period and for the same years 1,…,n that were used for calculating the amounts of capital employed. The average annual return for the calculation period is obtained by transforming formula (3) as follows
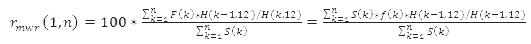
The MWR method has only been used to calculate averages for periods consisting of whole calendar years.
The index values H(k-1,12) and H(k,12) are the cost of living index values calculated for December in the years k-1 and k. Thus, the annual average rate of return for the calculation period is the average of the real annual rates of return weighted with the capital employed.
The average real returns adapting the TWR method are obtained from group-specific or system-specific nominal rates of total return f(k) calculated for each period by transforming formula (4) as follows
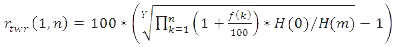
The duration of the calculation period is Y years and the interpretation of the index values H(0) and H(m) is the same as in the insurer-specific formula (5).
The TWR method can also be used for calculating real return averages for periods that have extra quarters at the beginning or end.
When a formula is applied, this is mentioned, for instance, in the footnote to the graph or table published.
Recommendation for the public reporting of the average return on an individual pension insurer’s investments for periods exceeding one year
The Investment Reporting Group recommends that, once a calendar year has ended, the average nominal returns per year are publicized not only for that year but for at least the past five and ten years as well. The average return for the latest five-year period can be reported after the 1st–3rd quarter of the year (”rolling”).
Some pension providers have gone through a fusion, fission or some other metamorphosis over the years; in consequence, as yet periods exceeding 10–12 years are not always possible for all insurers. However, insurers may choose to report the average nominal rate of return for a calculation period longer than ten years.
The nominal average rates of return are calculated using formulas (1) and (2).
The Investment Reporting Group’s recommendation does not include regular reporting of short-term or long-term real returns. In practice insurers may, for different reasons and in different circumstances, determine that the reporting of real returns is justified. In that case, the real rates of return for five-year and ten-year periods are the first to be reported. Naturally, insurers may also choose to report the average real rate of return for a calculation period longer than ten years.
The real average rates of return are calculated using formulas (1) and (5).
The guidelines “Calculating the average return for earnings-related pension investments” were approved by TELA’s Investment Reporting Group in October 2011. The guidelines can also be downloaded as a PDF file.

